Ocean Wave Simulation
In late 2023, I began working on a personal game project based around traversing the ocean. Since the ocean simulation was a main focus of the game, it needed to be both flexible enough to dynamically control the ocean state and detailed enough to represent a wide variety of weather conditions - all while running in real-time. Although I never finished the rest of the game, I consider the ocean simulation itself to be my proudest achievement as a programmer.
Initially, I tried using a few layered Gerstner waves (waves with both vertical and horizontal displacement) to simulate the ocean, but the results were lackluster. The combined result was not very detailed, and since I was simulating the waves on the CPU, I could only add so many waves before performance started to degrade.
Luckily, I came across two videos by Acerola and Jump Trajectory which describe a technique based on the fast Fourier transform (FFT) algorithm that can simulate many thousands of waves in parallel on the GPU. There's a good amount of math involved, but basically, we take advantage of the inverse Fourier transform's ability to convert a set of wave frequencies into actual waves. This means that if we can find out the overall distribution of wave frequencies in the ocean, we can convert that into an accurate representation of the ocean. Lucky again, there are already formulas available that can give us an oceanographic spectrum from a set of parameters like wind speed, wind direction, ocean depth, etc.
I used the JONSWAP ocean wave spectrum function and a Cosine-2s directional spreading function to generate the frequency domain representation of the initial ocean state. The result is a texture where wave frequency is represented as the distance from the center, wave direction is the direction from the center, and a complex amplitude is stored in the red and green channels of each pixel. The red and green channels are also multiplied by random gaussian distributed noise to create a natural distribution of wave phase and amplitude. There's another step that involves generating an additional complex conjugate version of the frequency spectrum, but I won't get too much into that.
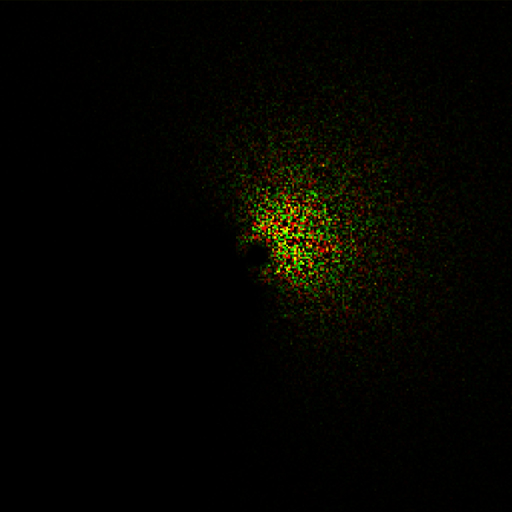
After generating the frequency domain of the initial ocean state, we advance the frequencies forward in time by using Euler's formula (and some other math) to rotate each pixel around the complex plane. The resulting Fourier components texture can be run through an inverse FFT (IFFT) to become the heightmap of the ocean at the specified time, but before we do that, we can derive additional Fourier components textures for the horizontal displacements of the Gerstner waves and for the slope on each axis (for normal mapping) using a few complex multiplications.
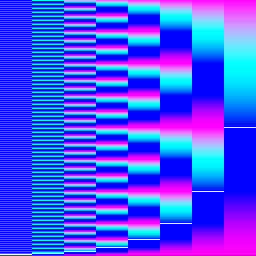
Finally, we run each fourier components texture through a 2D IFFT algorithm on the GPU to generate the X, Y, and Z displacements along with derivative maps to be used as fragment normals. I implemented the IFFT using a compute shader version of the Cooley-Tukey FFT algorithm as described by Fynn-Jorin Flügge in his thesis paper. This involves pre-computing a "butterfly texture" that contains the "twiddle factors" for each stage of the divide and conquer algorithm. The butterfly texture is then used in another compute shader for the horizontal and vertical IFFT pass on the fourier components textures.
There is still one glaring issue with this solution: tiling. If the grid length is set too small, the waves will prominently tile. Of course, we could simply set the grid length to cover a massive area, but the smaller details are lost unless we crank up the texture resolution as well. Instead, I used the same technique as in the Acerola and Jump Trajectory videos where we split the frequency domain into multiple cascades for the low, medium, and high frequency waves. The inverse FFT is performed for each of the frequency cascades so that we can layer each displacement map on top of each other at different scales. The effect of this is that the large waves tile over a much larger area, and the smaller waves that tile more frequently are layered on top. Even with only three cascades, the effect of tiling is almost eliminated while the fine details are preserved, and since the FFT is so fast, we can afford to triple the number of FFTs computed each frame as long as the texture resolution is kept at a reasonable level.